People: Kerry Corbett, Murray Hamilton
4 Semiconductor laser dynamics
|
The diode whose output wehave obtained our preliminary results is a GaAs diode with output around 830nm. Its output beam passes through an optical isolator and part is directed to a grating spectrometer and part to a high speed photodiode (BW = 6GHz). With the former we can study the laser spectrum and with the latter, the spectrum of the intensity fluctuations of the laser. An example of the data obtained with the spectrometer is shown below. The data obtained for the spectrum of the intensity fluctuations are in broad agreement with the multimode model results shown in figure 4.2 below.
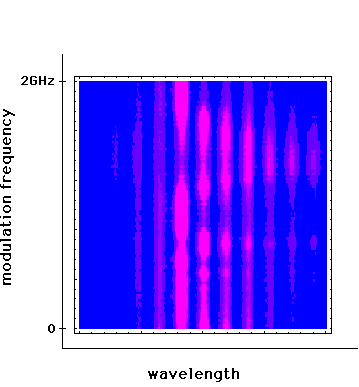
Fig 4.1 . Data showing laser spectra obtained with a grating spectrometer, with the exit slit replaced by a photodiode array, for several modulation frequencies showing the complex multimode behaviour of the laser when modulated at the relaxation oscillation frequency. When the modulation frequency is close to the relaxation oscillation frequency the laser becomes distinctly multimode. Although the laser appears to be single-mode at other modulation frequencies, there is still much more power in the "side-modes" than is the case for no modulation. The data also shows the shift in peak wavelength as the relaxation oscillation is excited.
For small amplitude modulation the rate equations can be approximated by a linear damped oscillator exhibiting a resonance at a characteristic frequency fRO. This frequency corresponds to the frequency at which the system oscillates as it approaches its steady state. For larger amplitude modulation we find that this frequency is tuned to a lower frequency as the modulation amplitude is increased. The behaviour of this resonant frequency is intimately linked with the bifurcations that the system undergoes. Since the noise inherent in the system acts to continually perturb it from its stable state then the transient frequencies will become amplified in the power spectra. One consequence of this is that these frequencies are readily detectable in experiments and can be used as a means to probe the dynamics of the system; in particular the various bifurcations which the system may undergo.
The single mode rate equations are well known in the literature and can be solved, with and without additive Langevin noise terms , and driving terms. We find that in the numerical solution of these equations period doubling bifurcations and chaos are predicted, but are not observed in the experiments, neither ours nor those of other workers. This model does correctly predict, at least qualitatively, the pulling behaviour of the relaxation oscillation peak in the intensity noise power spectrum, to the driving frequency or its subharmonic as the driving strength is increased.
We in fact use a more sophisticated model than the single mode model. Two main modifications are made; the model allows for multiple longitudinal modes and the dependence of the gain on the carrier density is taken into account more realistically. In a semiconductor laser photons are generated by the recombination of a conduction band electron and a valence band hole. We consider a two band model of the semiconductor laser active region with parabolic bands. Population inversion is achieved by pumping electrons into the conduction band and holes into the valence band. The gain depends on the distribution of carriers in the bands and so depends strongly both on the temperature and the carrier density in the active region. The peak gain occurs at different wavelengths for different carrrier densities with important consequences for the dynamics of the laser under modulation. The multimode rate equations used are from Tarucha and Otsuka (1981). In these equations the gain is approximated by a quadratic function of fixed shape. However in our work, both the peak gain and its position in wavelength are made functions of the carrier density. In order to consider the effects of the laser noise we add Langevin noise terms FN(t) and FPj(t) to the multimode rate equations. In the simulations, generally 25 modes were used. However, in most cases it is only the central modes, near the peak of the gain curve that have any significant amplitude. Figure 4.2 below shows results for the multimodel model illustrating a period doubling bifurcation. The behaviour is qualitatively similar to the results obtained for the single mode model where the relaxation oscillation peak is tuned (or pulled) to half of the modulation frequency before the onset of the period doubling bifurcation. We find however that for realisitic ranges of parameters that the first period doubling bifurcation is the only one predicted by the multimode model which is in better agreement with experiment (in contrast to the period doubling cascades to chaos predicted by the single mode model).
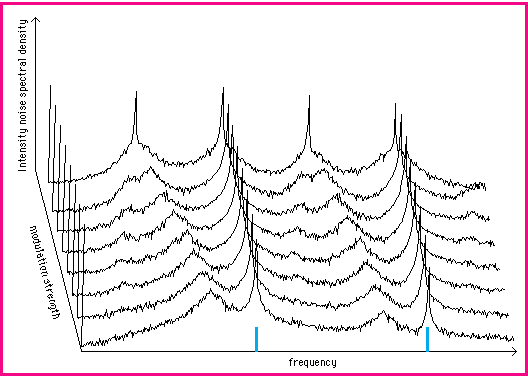
Figure 4.2 Consecutive power spectra of the total photon density exhibiting a period doubling as the modulation index is increased from m=0.4 to m = 0.75. The injection current is Ib=1.5. The vertical bars on the horizontal axis indicate the modulation frequency (2GHz) and its second harmonic. The low peak to the left of the peak at the modulation frequency is the (incipient) relaxation oscillation. As the modulation index is increased this peak is pulled toward the subharmonic frequency of the modulation. We can also calculate the laser spectrum (as opposed to the spectrum of intensity noise) which can be compared with Fig 4.1. A typical result is shown below in figure 4.3. A prediction of the model is that as the modulation frequency or one of its harmonics is tuned through the relaxation oscillation frequency the system becomes multimode with the spectrum shifting towards the shorter wavelength modes. The reason for the occurence of this phenomena can be partly understood by considering the effect that the phase change, experienced by the carrier density as the system passes through a resonance, affects the gain and hence the photon density of the modes themselves. This is consistent with what is observed in experiments.
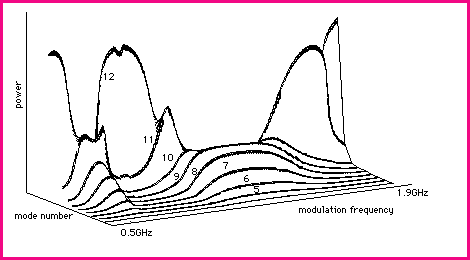
Figure 4.3. Calculated powers of the modes as a function of modulation frequency for modulation index m=0.4 and injection current Ib=1.5. The modes are labelled 5 - 12, the numbering being arbitrary. Another difference between the two models is the occurence of a Hopf bifurcation in the multimode model. This phenomena results in the appearance of extra peaks in the power spectra of intensity fluctuations and generally occurs for modulation frequencies near the relaxation oscillation. No experimental observations of this phenomena have been made to date in these experiments and it is quite possibly an artificial feature. Further work needs to be done on this matter.
|
- to contents
- to part 1 (overview)
- to part 2
- to part 3
References
S Tarucha and K Otsuka (1981), IEEE J. Quantum Electron. QE17, 810