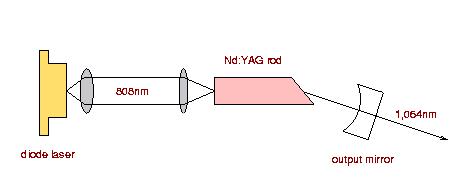
|
|
 The interaction of these gives rise to some interesting effects,
whereby the laser can operate in an antiphased regime. This means
that individual longitudinal modes have fluctuations that, at certain
frequencies, cancel the fluctuations of the other longitudinal modes.
At other frequencies, typically just one, the fluctuations all add up
in phase. This results in relatively simple total behaviour: the
fluctuation spectrum looks like that of just a single oscillator
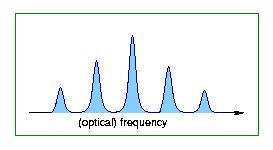
rather than an array. That is it would show just one peak. If we look
at the fluctuation spectrum of just one of the longitudinal modes,
which can be separated out of the laser beam with a Fabry-Perot
interferometer, we see a multipeak spectrum that is characteristic of
the array.
The interaction of these gives rise to some interesting effects,
whereby the laser can operate in an antiphased regime. This means
that individual longitudinal modes have fluctuations that, at certain
frequencies, cancel the fluctuations of the other longitudinal modes.
At other frequencies, typically just one, the fluctuations all add up
in phase. This results in relatively simple total behaviour: the
fluctuation spectrum looks like that of just a single oscillator
rather than an array. That is it would show just one peak. If we look
at the fluctuation spectrum of just one of the longitudinal modes,
which can be separated out of the laser beam with a Fabry-Perot
interferometer, we see a multipeak spectrum that is characteristic of
the array.
|
|
|