skip to part 2 (diode laser)

1 Overview and Aims

The subject of the research described below is the search for an understanding of the limitations imposed by nois and other fluctuations on nonlinear systems. Specifically, the research comprises a study of the effects of external noise in in certain nonlinear optical phenomena. The experiments involved semiconductor lasers and miniature Neodymium lasers which can show nonlinear effects if pushed into certain regimes of operation and are "clean" systems in that they are relatively insensitive to unwanted environmental perturbations.

It is a general fact that nonlinear processes are sensitive to noise, often in quite complicated and poorly understood ways. This has been a very active area of theoretical research for some time now, but good quantitative experiments have been quite rare. This is surprising in view of the increasing use of nonlinear techniques in applications, especially in optics.

This work is also of fundamental interest because in science one usually tries to exclude noise and fluctuations from an experiment for the sake of "clean data". Yet fluctuations are ubiquitous in nature and they often lead to qualitative differences in many phenomena, especially nonlinear ones. Thus it is important to push our understanding beyond the noise free case.

The aims were thus;

i) To investigate the effect of noise on the dynamics of a small diode laser driven Nd:YAG laser. The driving signal is easily modulated to excite the relaxation oscillations and chaotic behaviour of the Nd:YAG laser. Noise can be added to the modulation in a straightforward way.

ii) The somewhat more complicated dynamics of a diode laser are investigated in a similar fashion to the above. Extra complications arise because the active species (an electron-hole pair) is mobile, unlike the Nd ions in the Nd:YAG case. Space-charge like effects also play a role in the behavior of these lasers.

iii) A further objective in both of these experiments arose because of recent work in the field of nonlinear prediction techniques (Weigend and Gerschenfeld 1994). The use of these techniques, which permit the extraction of the attractor topology from chaotic data, will help us to test our understanding of the dynamical variables in lasers. Conversely we will be able to test the robustness of these techniques to noise, since one of the objectives in nonlinear dynamics is to be able to distinguish noisy from chaotic data.

One of the things that became apparent as this research progressed was that the multimode nature of the lasers was very important. Besides the more prosaic problem of needing to take this into account to explain the phenomenology, the multimode nature of the lasers makes them ideal examples for the study of arrays of coupled nonlinear oscillators. If several cavity modes are excited they can be coupled, typically through the position dependent gain-sharing that is caused by the standing wave nature of the electromagnetic field for a Fabry-Perot resonator (Tang et al. 1963) or through the inclusion of a nonlinear crystal for frequency doubling in the cavity (Wiesenfeld et al. 1990). Oscillator arrays are a popular subject for theoretical studies because they are a bridge between relatively simple systems, and more complex systems which require statistical techniques and which show "emergent properties" that require the introduction of concepts that have no direct connection to fundamental ideas. They can show a variety of phase locking phenomena such is antiphase dynamics where the phases of the oscillators are clustered in one of several identified patterns (Wang et al. 1995, Hadley et al. 1988) so that interference destroys the response at all but one of the coupled system eigenfrequencies. This became a significant part of this research.

Direct experimental confirmation of the phase clustering has been found for a three mode laser in a limit cycle regime (spiking) (Otsuka et al. 1993). For a laser in steady state operation, noise, either intrinsic or deliberately introduced, has been exploited to excite the various collective modes. In the intensity noise power spectrum for the individual laser cavity modes one sees peaks corresponding to collective modes that are absent in the spectrum for the total intensity (Mandel et al. 1996). The latter spectrum typically shows just one remaining resonance which is the relaxation oscillation of the laser and has the highest frequency of the collective modes. However the measurement of power spectra discards phase information, and the clustering cannot be verified directly in this technique.

We took a different approach, exciting the collective modes with a sinusoidal modulation of the laser pumping rate and measuring the response of the laser at the excitation frequency for both the total laser intensity and the individual laser modes. This is the transfer function method, which is well known in engineering and has been advocated and used (Khandokhin et al. 1996) for theoretical analysis of this problem. The magnitude of the transfer function has also been measured (Golyaev and Lantratov 1979), but as far as we are aware this is the first experimental measurement of the full complex transfer functions for the study of antiphase dynamics in lasers. Knowing the phase and magnitude of the transfer function, information on the contributions of each cavity mode to each of the collective modes can be extracted by determining the residues, as will be discussed below. Typically the cancellation of the collective modes in the antiphase dynamics about a steady state is not perfect and by measuring transfer functions the degree to which cancellation occurs can be ascertained as can the type and extent of the clustering.

2 The Nd laser

2.1 Laser construction

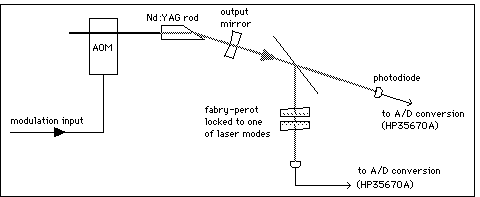
The basic laser construction is illustrated in Figure 1.

The laser medium that we used was a Nd:YAG rod cut with one end perpendicular to the rod axis and the other at Brewster's angle. A high reflection coating on the perpendicularly cut end formed one end mirror of the laser cavity and the output coupler was a partially transmitting mirror (T=1%) mounted on a piezoelectric tube for fine cavity length control. The Brewster cut face served to ensure that all modes were linearly polarised in the same plane. The Nd laser was end pumped by a 40mW diode laser through the coated end of the rod (T=65% at 808nm). The optical path length of the cavity was 24.3mm corresponding to a longitudinal mode separation of d[nu] = 6.16GHz. Modulation of the pump was achieved with an acousto-optic modulator which avoided the mode partition noise of the pump laser that can occur if its injection current is modulated. We also had an optical isolator, comprising a polariser and Fresnel rhomb, between the pump laser and the Nd laser to minimise the destabilising effects of optical feedback.

2.2 Early experiments

Initial experiments consisted of modulating the pump laser intensity at or about the frequency of the laser relaxation oscillation, thus exciting this oscillation and if the modulation were strong enough, exciting chaotic behaviour in the total laser intensity, as recorded with an A/D converter. When the pump laser intensity was modulated at or close to the relaxation oscillation frequency, or one of its sub-harmonics or harmonics, pulsed (limit cycle) and chaotic output power from the Nd:YAG laser could be achieved depending on the strength and frequency of the modulation. One of the early experiments with this intial setup was to record chaotic intensity data and then apply singular value decomposition to recreate a model of the chaotic attractor. This showed that the attractor could be embedded in a three dimensional space, i.e. its dimension was less than three. Subsequently the output of the laser was checked with a scanning Fabry-Perot interferometer and shown to be multimode, with between 2 and 7 longitudinal modes running simultaneously. This implies that number of degrees of freedom was in fact rather larger than the embedded attractor would suggest and that somehow several of these were being "frozen out" of the dynamics.

2.3 Transfer function measurements

In order to analyse the multimode behaviour we measured transfer functions for the total intensity and the intensities individual laser modes. Operationally, this means that we modulated the pump input over a range of frequencies and measured the amount of the modulation frequency in the intensity in question. The strength of the modulation was small so that the laser remained close to steady state. The output of the Nd laser was split into two beams so that the total intensity and intensity of one mode could be measured simultaneously. With a pump level of around 1.3 times threshold we observed between four and six laser modes, depending on the exact cavity length. The data shown below is for five mode operation. A Fabry-Perot interferometer was used in one output beam to select individual laser modes. The intensities, total and modal, were measured with low noise photodiode detectors and the outputs of these were directed to a Hewlett Packard HP35670A signal analyser. For transfer function measurements the analyser supplies the modulating signal, scanned repetitively in frequency.

A transfer function can be expressed either as a ratio of polynomials (pole-zero representation) or as a partial fraction (pole-residue representation) (Blackman 1977):

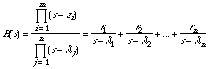(1)

The poles [lambda]_j are the eigenvalues of A, the zeros are z_i and the residues are r_j . Interesting insights into the problem can be gained from both the pole-zero representation and the pole-residue representation. The latter gives a particularly vivid picture of the operation of the antiphase dynamics as the residues contain information about the contribution of each oscillator to the collective modes.

In our experiment a parallel theoretical analysis is made. Although the residues are determined by fitting a general transfer function, in the form of a ratio of polynomials, to the data, we can also calculate the residues on the basis of a suitable theoretical model. It turns out that the comparison of the measured and calculated functions is quite a sensitive test of the model.

We start with the rate equations due to Tang, Statz and deMars (1963), modified slightly to include the small pump rate modulation w = msin[omega]t. These equations are appropriate to a Nd:YAG laser with a high finesse Fabry-Perot cavity and take into account the spatial holeburning. It is assumed that the inversion density, averaged over a few optical wavelengths, does not vary along the laser medium in a direction parallel to the axis of the laser mode. Also implicit in these equations is the assumption that the laser medium fills the cavity. These assumptions are not strictly valid for our laser, but in the present absence of a better model the TSdM equations are still useful to illustrate how our measurements of transfer functions can discriminate against a model.

For comparing the measured transfer functions to the theory, several parameters needed to be determined. We measured the cavity lifetime to be [tau]_c =3.56ns and took the response time of the medium to be [tau]_f =230us (Koechner 1992). For the gains [gamma]_i we assumed a Gaussian distribution of width 135GHz, normalized to one at the peak and with an adjustable offset of the comb of cavity modes from the center of the gain profile.

The transfer functions are complex valued and contain phase and magnitude information about the response of the modes or total intensity. The residues are extracted by fitting general transfer functions in the pole-zero representation to the data and converting the fitted functions to the pole residue representation. Table 1 below shows the residues extracted from the data for operation with pump power 1.3 times threshold and five modes lasing. For comparison we show the residues in table 2 calculated on the basis of the Tang Statz deMars equations. The frequencies shown are those of the poles.

Freq	13.3+/-0.1	kHz	18.7+/-0.1	kHz	25.6+/-0.1	kHz	34.6+/-0.7	kHz	96.1	kHz
	Mag	Phase	Mag	Phase	Mag	Phase	Mag	Phase	Mag	Phase
Mode I	851.7	71.0	246.3	65.6	908.3	74.1	1739.0	51.0	27314	-177.2
Mode II	846.8	-103.2	135.1	-117	2267.8	66.0	268.9	-110.6	20031	-177.2
Mode III	251.9	-98.3	95.5	-130.6	1939.9	-119.8	959.0	57.4	15692	-174.4
Mode IV	653.3	-108.4	230.0	67.3	1405.0	-119.7	1212.9	-131	15658	-179.3
Mode V	1285.4	73.9	68.65	5.1	184.0	55.0	1480.8	-129.2	15561	-174.6

The antiphase dynamics manifests itself as a double clustering of the residue phases. The agreement between the experiment and the calculated transfer functions is not perfect. The predicted and measured pole frequencies do not completely agree. Furthermore, comparing the clustering of calculated and measured residues more closely we can see more discrepancies. In the theory based on equations (1) the phases of the contributions to each resonance from each cavity mode follow a sequence (+ + + + - ), (+ + + - - ), (+ + - - - ), (+ - - - - ), (- - - - - ), as we look at each collective mode in turn. A similar ordering of the phases has been previously reported in a numerical analysis of a multimode laser with feedback [Pieroux et al.1994]. The data do not show this ordering. This, we believe, reflects an inadequacy of equations (1) in that they do not take into account the exponential decay of the inversion density along the optical axis due to the absorption of the pump light. Further, the gain medium in our laser does not fully occupy the optical resonator.

Work to resolve the discrepancies by taking into account these factors is currently in progress. We conclude from this study that the transfer function approach gives much more detailed information and is a more sensitive means of studying the dynamics of the modes than excitation with broadband noise.

to title page

to part 2

References

F. Blackman (1977) Introduction to State-variable Analysis (Macmillan Press, London )

Yu. D. Golyaev and S.V. Lantratov (1979), Sov. J. Quantum Electron. 9 1390

P. Hadley et al. (1988), Phys. Rev. B38 8712

P. Khandokhin et al. (1996), Opt. Commun., 123 372

W. Koechner (1992) Solid State Laser Engineering, 3rd Edn. (Springer, Berlin )

P. Mandel et al. (1996), Phys. Rev. Lett. 76 2694

K. Otsuka et al. (1993), Jpn. J Appl. Phys. 32 L318

L Stamatescu and M Hamilton (1997) Phys. Rev E55 2115

D. Pieroux et al. (1994), Opt. Commun. 108 273

C.L. Tang et al. (1963), J. Appl. Phys. 34 2289

J-Y. Wang et al. (1995), Quantum Semiclass. Opt. 7 169

Weigend and Gerschenfeld (1994) Predicting the Future, Proceedings of NATO Advanced Research Workshop , Santa Fe, 1992 (Addison Wesley)

K. Wiesenfeld et al.(1990), Phys. Rev. Lett. 65 1749